
This article was originally published in Hebrew in the internet magazine Haayal Hakore – the best Hebrew website!
 | |
Johann Sebastian Bach | |
As the title of The Well-Tempered Clavier hints, Bach composed it for keyboard instruments that were
tuned (or tempered – I shall use the two terms interchangeably below, even though they are not
exactly the same) in a certain way – a way that was considered revolutionary at the time. Why
is there more than one way to tune the keyboard? In this article I attempt to answer this question,
and in particular, to describe how modern musical instruments are tuned.
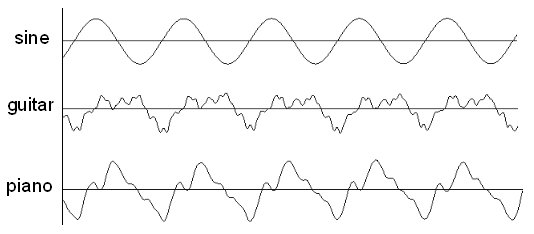
The upper waveform – the simplest of the three – was created by a computer, and it can be heard in example 1. This waveform corresponds to a basic mathematical function called sine, and perhaps this is why it sounds “synthetic” or “boring.” Waveforms of real musical instruments are much more complex – the second waveform is of a guitar (example 2), and the third, of a piano (example 3). All three waveforms are periodic – they are made of a certain “basic unit” that repeats itself again and again; they differ only in the shape of this basic unit. These shape differences are the main (though not the only) factor that determines the timbre (“sound color”) of the note – through them we can tell the difference between the sound of a violin and that of a trumpet, for example.
The number of cycles a wave completes in a second is called its frequency, and the unit used to measure frequencies is called Hertz (abbreviated to Hz). The higher the frequency is, the shorter is the basic unit, and the corresponding note has what we call a higher pitch. The three notes we have heard had the same frequency – namely, 440 Hz – and musicians named this frequency A; for historical reasons, it is customary to tune musical instruments relative to this note, and we will therefore see the number 440 again and again in this article. At its best, the human ear can detect notes whose frequency is between 20 and 20,000 Hz. Unfortunately, this range shrinks significantly as one gets older, and its upper limit usually drops below 10,000 Hz after the age of 55. For comparison, the audible range of mice is 1,000–91,000 Hz, and that of elephants is 16–12,000 Hz.
 | |
Pythagoras | |
Pythagoras and his disciples developed an entire theory that connects numbers, musical notes, and the motion of planets. Large parts of this theory are dismissed today as an esoteric mysticism, but those that deal with the mathematical regularity behind musical notes constitute to this day, about 2,500 years after they were formulated, the basis behind the theory of music.
A sequence of notes, played one after the other, is called a melody. Listen to the very short melody in example 6. It is built from three notes, whose frequencies are 440, 660, and 733.3 Hz. Now listen to example 7, whose note frequencies are 550, 825, and 916.6. Is this the same melody? Even though the two melodies used totally different notes, we easily recognize that this is “actually the same melody.”
What made us feel that this is “actually the same melody”? The key word is once again ratios. The human ear and brain, it turns out, recognize two note sequences as “the same melody” when the ratios between their note frequencies are kept the same. And this is indeed exactly what happened: In both melodies, the ratio between the first and the second notes is 2:3, and the ratio between the first and the third is 3:5.
Both the human voice and musical instruments are limited in the range of frequencies they can produce. Often a singer, for example, prefers to sing a melody “higher” – or in the musicians parlance, in a higher key – because he or she finds it physically difficult to sing the low notes. The mathematical meaning of this change should now be clear: the list of frequencies the singer will sing will be the list of the original frequencies, multiplied by a constant (that should be greater than one, if we want the new melody to be higher). This procedure of changing a key is called transposition.
If we listen to a melody played at the same time in two different keys, the result will usually sound odd, as example 8 shows. In this example, the melody whose note frequencies are 440, 660, and 733.3 Hz was played together with the one whose note frequencies are 550, 825, and 916.6 Hz. But if the two melodies are exactly one octave apart (that is, the note frequencies of the one are exactly twice those of the other), the result will sound rich and pleasing to the ear (example 9; one melody’s frequencies here are 440, 660, and 733.3 Hz, and the other’s are 880, 1320, and 1466.6 Hz).
The human ear treats notes that are an octave apart as “the same thing” in a very strong sense, to the point that musicians give them the same name. Recall that the note whose frequency is 440 Hz is called A; this is indeed also the name of the note one octave higher (880 Hz), two octaves higher (1760 Hz), one octave lower (220 Hz), etc. Since notes that are exactly one octave apart – or more precisely, an integer number of octaves apart – are related so strongly to each other, composers and musical arrangers often double the original melody, by playing in parallel a copy of it, one octave higher (or lower), sometimes with different musical instruments. This creates a rich effect of “thickness,” as can be heard in example 10 and example 11.
Different musical instruments produce notes in different ways. From a violin, for example, even if it has only one string left, one can produce infinitely many notes: a note’s pitch is determined by the point the violinist places her finger on the violin’s fingerboard, and since the fingerboard is smooth, the violinist may place her finger anywhere she likes, and produce infinitely many different notes.
Keyboard instruments such as the piano, on the other hand, have only a limited number of keys, and can therefore produce only a limited number of notes. Which notes should they be, then? Let’s try to answer this question, and restrict ourselves to the octave between 440 and 880 Hz. We start by putting inside the “frequency basket” – the set of notes we want our keyboard to produce – the frequency 440 Hz. If we want to be able to play the Pythagorean ratios, then we certainly need to add to the basket the frequency 660 Hz, since we saw that the ratio between 440 and 660 is 3:2; in other words: 660 is a perfect fifth above 440, we want to be able to play perfect fifths, and therefore 660 must be added to the basket. Another perfect fifth above 660 we find 990; this frequency is outside our range, but an octave below it there is 495, which is inside (and we want to be able to play octaves), so we add 495 to the basket as well. Another perfect fifth above 495 there is 742.5, which we add next, etc.
It can be shown mathematically (how?) that if we proceed this way, we will never “close the loop” and return to the note A (that is, reach the frequency 440), and will therefore need infinitely many notes in the desired range! This is a difficult problem, and generations of musicologists debated vehemently over how to solve it, and proposed multitude of ways for tuning the keyboard. Without getting into any of the details, I will only say that ancient keyboard instruments were usually tuned in a way that allowed them to produce a certain number of exact Pythagorean intervals, but as a result, it was not possible to play the same melody on them in different keys (that is, to transpose melodies).
The modern solution to the temperament problem sacrifices the ability to play precise Pythagorean intervals, in exchange to the ability to transpose perfectly. Its basic idea is to divide the octave into a certain number of equal musical intervals.
Suppose we wanted to divide the octave between 440 and 880 into two equal musical intervals. We saw earlier that the size of a musical interval is the ratio between the frequencies of its two notes, so we are looking for a number between 440 and 880, so that the ratio between this number and 440 is the same as the ratio between 880 and this number. A short calculation yields (how?) that the frequency of the note in the middle of the octave is 440 times the square root of 2, namely 622.25 Hz, and that the desired ratio is the square root of 2.
Similarly, if we wanted to divide the same octave into three equal intervals, we would get (how?) that the frequency ratio between two adjacent notes is the cube (third) root of 2. Thus, at the third of the way between 440 and 880 there is the frequency 440 times the cube root of 2, namely 554.37 Hz, and at two thirds of the way there is this latter frequency, times (again) the cube root of 2, namely 698.46 Hz.
Using this method we can divide the octave into four, five, or any other number of equal intervals. It’s important to understand that once we divide the octave in a certain way, we immediately get also the note frequencies in the other, adjacent octaves – when we divided the octave into three equal intervals, for example, the frequencies that we will get in the octave between 880 and 1760 are simply twice the frequencies we just found, namely, 880, 1108.73, 1369.91, and 1760 Hz.
The main advantage of dividing the octave into equal intervals is that it allows us to transpose perfectly: since we made sure that the ratio between adjacent notes in the partition is constant, we may take any melody that can be played on the keyboard we created, multiply its frequencies by this constant, and get another melody that can be played on our keyboard; this way we keep the ratios between the melody’s frequencies, and get “the same melody,” only in a different key.
The disadvantage of this method is that it allows us to play only one exact Pythagorean interval – the octave. It can be shown (how?) that no matter to how many equal musical intervals we divide the range between 440 and 880, the partition will never include the frequency 660, which, as you may recall, is a perfect fifth above 440. At first glance, this problem seems very serious – the Pythagorean intervals are of great musical importance, and we wouldn’t like to be unable to play them. The rescue, surprisingly, comes from the limitations of the human ear: it is true that we will never be able to reach 660 exactly, but a careful partition of the octave into the “right” number of equal musical intervals, will include a frequency that is very close to 660 – so close, that we’ll have a hard time distinguishing between the two.
To how many intervals, then, should we partition the octave? The magic number, it turns out, is 12. If we divide the octave between 440 and 880 into 12 equal musical intervals (in which case the ratio between adjacent notes is the 12th root of 2), the resulting frequencies will be
| 440.00, | 466.16, | 493.88, | 523.25, | 554.37, | 587.33, | 622.25, |
| 659.26, | 698.46, | 739.99, | 783.99, | 830.61, | and 880.00. | |
As expected, 660 is not among these frequencies, but 659.26, which is only slightly lower, is. In example 12 we can hear these two notes, one after the other; can you tell which one of them is the lower? (answer is here). We can find in this list also close substitutes – though not as close – to the other frequencies from the frequency basket we built above.
This tuning method, in which the octave is divided into 12 equal musical intervals, is called equal temperament, and by the beginning of the 20th century it almost completely superseded a multitude of other tuning methods that were proposed throughout history. In contrary to the commonly held belief, this method was not the one for which Bach composed his The Well-Tempered Clavier. Bach, probably inspired by the musicologist Andreas Werckmeister, indeed divided the octave into 12 musical intervals, but these intervals were slightly different from each other; this method was considered innovative at its time, as it was among the first to allow a reasonable (though not perfect) transposition of any melody into eleven other keys.
To experience the differences, listen to the first four bars of the first prelude from Bach’s The Well-Tempered Clavier in the Pythagorean temperament (example 13), Werckmeister’s temperament (example 14), and the equal temperament (example 15). The differences in this case are not huge, since the piece was written in a key in which the Pythagorean temperament sounds best. If we play the same four bars in another key, the Pythagorean temperament (example 16) will indeed sound much worse than both Werckmeister’s (example 17) and the equal temperament (example 18).
Because Bach’s partition of the octave was not completely equal, some people claim that each of its keys has a distinct “color,” which is lost in contemporary musical instruments; thus, they say, it’s better to play musical pieces with the instruments that existed when they were composed. They are not the only ones who are dissatisfied with the equal temperament: for the intricate Arab music, it’s not enough to partition the octave into 12 intervals, so it is partitioned into 24 equal intervals; some people believe that western music should develop as well in microtonal directions, and partition the octave into 31 intervals (this is how it sounds), while others say that we should use technology to return to the pure Pythagorean temperament.
So what does the future hold? Prophecy, as we all know, is a difficult task, but it seems most
likely that the current situation will continue – the equal temperament will dominate, but
competing methods will find supporters outside the musical mainstream.
Thanks to Alon Amit for his help in preparing the graphs and sound samples.

Questions? Comments? Corrections? Feel free to contact me.

| © All rights reserved to Yuval Nov |